Geekdom

I've been out of the mathematical side of engineering now for quite some time now. As a result I sometimes struggle to solve tricky mathematical problems. So it came as a moment of triumph today when I managed to solve the following:

My colleague Emily wanted to know how many combinations could be made from a set of five objects, where you could not repeat any of the objects and where order didn't matter. For example, if you had the objects 1, 2 and 3, then the following combinations were available: 1, 2, 3, 12, 13, 23, and 123. That is, there are six. Now I know I could do them all by hand, but say for a large number of objects, eg 100, that would be a lot more tricky. So after trial and error I triumphantly came up with:

Number of combinations = Sum from 1 to i of nCi, where
i = the number of objects that can be chosen
n = the number of objects to choose from, and
C = the combinations derived from n!/((n-i)!*i!), where n!=n*n-1*n-2*...*n-(n+1)
or:






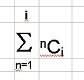
Solving this makes feel less thick, despite the fact that the maths are not that complex...

Yes, I know I'm a geek.

With a small car.